Eye Health and
Treatment Solutions
Test Eye Australia, your go-to resource for maintaining optimal eye health and managing common eye conditions.
Our Services
Eye Examinations and Vision Testing
Ensure the health of your eyes with our thorough eye examinations and vision testing services. Our experienced optometrists will assess your visual acuity, evaluate eye health, and detect any refractive errors or signs of eye diseases. Regular eye exams are essential for early detection and management of eye conditions.

Retinal Evaluation and Treatments
For retinal conditions such as diabetic retinopathy, macular degeneration, or retinal detachment, we offer comprehensive retinal evaluations and advanced treatment options. Our retinal specialists are dedicated to preserving retinal health and optimizing vision outcomes for our patients.
LASIK and Refractive Surgery
Explore options for vision correction with our LASIK and refractive surgery services. Whether you’re nearsighted, farsighted, or have astigmatism, our consultations will determine if you’re a candidate for LASIK, PRK, or other refractive procedures aimed at reducing or eliminating the need for glasses or contact lenses.
Glaucoma Screening and Management
Detect and manage glaucoma with our specialized screening and management services. Glaucoma is a serious eye condition characterized by increased pressure within the eye that can lead to vision loss if left untreated. Our team is experienced in diagnosing and treating various types of glaucoma to preserve your vision and prevent further damage.
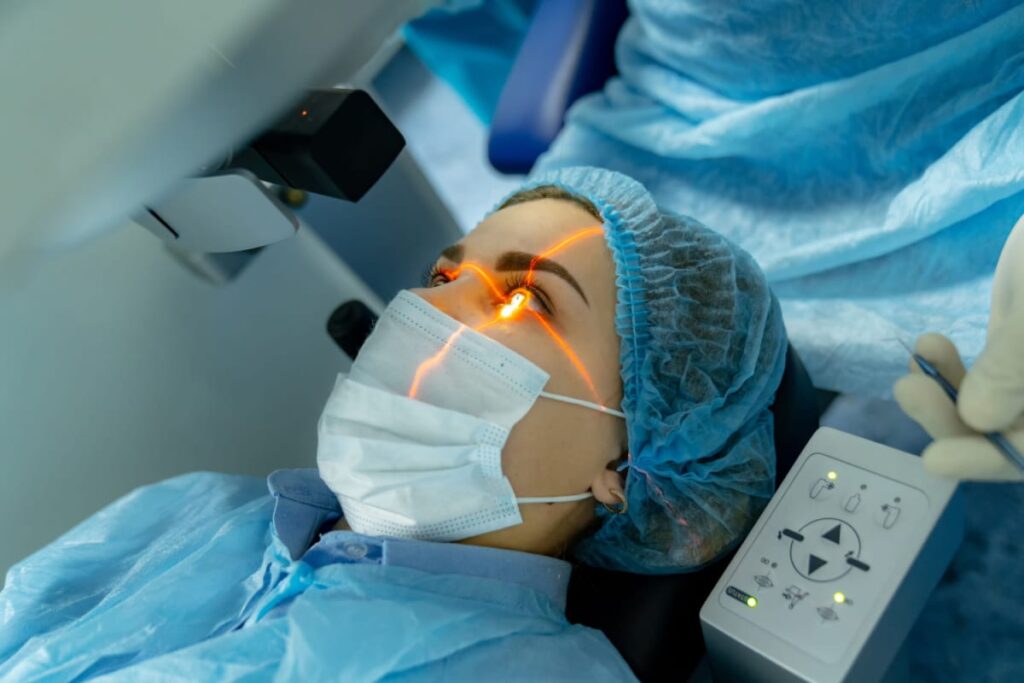
Cataract Evaluation and Surgery
If you’re experiencing symptoms of cataracts or have been diagnosed with this condition, we offer comprehensive cataract evaluations and surgical solutions. Our skilled ophthalmologists specialize in cataracts surgery, utilizing advanced techniques and intraocular lens options to restore clear vision and improve quality of life.
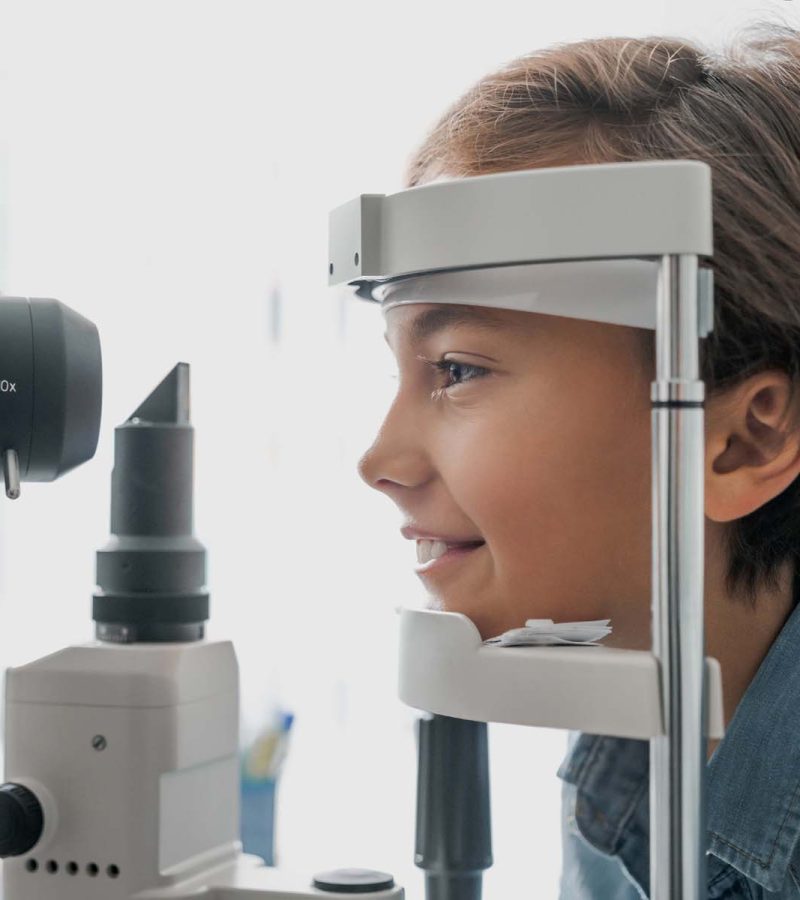

What Sets Us Apart
Expertise: Our team comprises experienced eye care professionals, including ophthalmologists, optometrists, and researchers, who contribute their expertise to ensure the accuracy and reliability of our content.
Comprehensive Coverage: We cover a wide range of topics related to eye health, from preventive tips and lifestyle recommendations to detailed insights into various eye conditions and treatment options.
Empowerment: We believe in empowering individuals to take charge of their eye health by providing reliable information, practical advice, and resources that enable them to make proactive choices for their well-being.



Start Your Journey to Better Eye Health
Whether you’re looking for guidance on maintaining healthy vision, exploring treatment options for a specific eye condition, or seeking preventive tips for protecting your eyesight, Test Eye Australia is here to assist you. Explore our website, engage with our content, and take proactive steps toward healthier eyes and clearer vision.
Popular Articles
Laser Eye Surgery vs Glasses and Contacts: Lifetime Cost and Lifestyle Comparison
Clear vision is essential for daily life, work, and hobbies. For busy professionals, active adults, and frequent travelers, the decision between laser eye surgery and […]
How to Access Funded Services with Occupational Therapy NDIS
Accessing funded services through the National Disability Insurance Scheme (NDIS) can be a transformative experience for individuals with disabilities, particularly when it comes to occupational […]
Making Everyday Routines Easier with Occupational Therapy at Home
Occupational therapy (OT) is a vital healthcare profession that focuses on helping individuals achieve independence in their daily activities. Whether recovering from an injury, managing […]
Perfect LASIK Surgery: Myths vs. Facts You Should Know
Introduction If you’ve ever worn glasses or contacts for years, the idea of perfect LASIK surgery might sound almost too good to be true—seeing clearly […]
Oxygen Concentrator Philips Everflo: FAQs and Tips
The Philips Everflo oxygen concentrator is a popular choice for individuals requiring supplemental oxygen. Renowned for its reliability and efficiency, this device has become a […]
How to Use the Philips Everflo Concentrator Safely at Home
The Philips Everflo Concentrator is a reliable and efficient device designed to provide oxygen therapy for individuals with respiratory conditions. With its user-friendly design and […]
Contact us today to learn more about Test Eye Australia
Get in Touch
Whether you’re seeking information about a specific eye condition, exploring treatment options, or simply looking for tips on maintaining healthy vision, Test Eye Australia is here to assist you. Contact us with your questions or concerns, and let us help you take proactive steps toward better eye health.